【MediaPipe×Python】上肢の肩関節外転を可視化して解析する方法｜ピクセル座標から定量評価

✅ はじめに｜肩関節の動きの定量化

リハビリで重要な要素には「肩関節の可動域（外転や挙上）」があります。
通常の場合は目視による評価が一般的ですが、動画を用いた骨格推定を行うことで、動作を数値客観化して定量することが可能です。

今回は、前回の記事で使った「mediapipe＋ピクセル座標CSV（http://ktr-project.net/?p=46）」を活用して：

✅ 左右の肩の最大外転・肩峰挙上それぞれの角度を算出
✅ スティックピクチャで動作前後の差を可視化
✅ 結果を角度（°）として出力

までを一貫して行います！

✅ 使用データ：前回の記事で生成したCSV

本記事では、以下のようなCSVを使用します。前回の記事で生成された各関節のピクセル座標の時系列データのことを指します。

mediapipeで出力したデータのヘッダーはこんな感じになっています。

frame, x_11_px, y_11_px, x_13_px, y_13_px, x_15_px, y_15_px, ...

いろいろな関節座標がありますが、今回使用するランドマークは次の番号のものになります。mediapipeの関節位置座標の番号は、mediapipe poseの公式HPにかいてあるので、他の座標を使いたい場合には、そちらを参照するようにしましょう（URL: https://github.com/google-ai-edge/mediapipe/blob/master/docs/solutions/pose.md）。

ランドマーク	番号	説明
11	左肩	left shoulder
13	左肘	left elbow
15	左手首	left wrist
12,14,16	右上肢も同様です

✅ 解析の基本方針

🎯 可動域をどう定義するか？

タイプ	角度の定義
肩関節外転	肩→肘のベクトルと、垂直下方向ベクトルのなす角
肩峰挙上	左右の肩のラインと、水平右方向ベクトルのなす角

MediaPipeの骨格推定は、2D平面上のピクセル値で表現されるため、この方法で傾きや肩関節の角度を定量化できます。

✅ Pythonコード全文

以下が、左右の上肢の可動域を解析・可視化する完全コードです。ちょっと長いですが、基本的な処理のフローとしては、

　①csvデータを読み込み→②使用するデータの抽出→③角度計算→④最大外転のタイミングの取り出し→⑤スティックピクチャによる描画になっています。

あんまり整理されていなく、重複している処理も多いですがご了承ください。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
# --- 角度計算用関数 ---
def calangle(v1, v2):
    """2つのベクトル間の角度（度）を計算"""
    dot = np.dot(v1, v2)
    norm1 = np.linalg.norm(v1)
    norm2 = np.linalg.norm(v2)
    if norm1 == 0 or norm2 == 0:
        return 0.0
    return np.degrees(np.arccos(dot / (norm1 * norm2)))

# --- CSV 読み込み ---
csv_path = "pose_output_pixel.csv"
df = pd.read_csv(csv_path)
n_frames = len(df)
n_landmarks = 33

# 各ランドマークの x, y 座標を numpy 配列に格納（ヘッダー "x_i_px", "y_i_px"）
pos_data_x = np.zeros((n_frames, n_landmarks))
pos_data_y = np.zeros((n_frames, n_landmarks))
for i in range(n_landmarks):
    pos_data_x[:, i] = df[f"x_{i}_px"].values
    pos_data_y[:, i] = -df[f"y_{i}_px"].values

# ------------------------------
# 各部位の座標（そのままの値を使用）
# ------------------------------
# 頭部中心: ランドマーク 2 と 5 の平均
mid_head = np.array([
    (pos_data_x[:, 2] + pos_data_x[:, 5]) / 2,
    (pos_data_y[:, 2] + pos_data_y[:, 5]) / 2
]).T

# 左上肢
l_shoul = np.array([ pos_data_x[:, 11], pos_data_y[:, 11] ]).T
l_elb   = np.array([ pos_data_x[:, 13], pos_data_y[:, 13] ]).T
l_wri   = np.array([ pos_data_x[:, 15], pos_data_y[:, 15] ]).T

# 右上肢
r_shoul = np.array([ pos_data_x[:, 12], pos_data_y[:, 12] ]).T
r_elb   = np.array([ pos_data_x[:, 14], pos_data_y[:, 14] ]).T
r_wri   = np.array([ pos_data_x[:, 16], pos_data_y[:, 16] ]).T
# ------------------------------
# 各角度の計算（全フレームで算出）
# ------------------------------
# 左肩外転角：左肩から左肘へのベクトルと、垂直下向きベクトルとの角度
# ※画像座標系では y は下方向に増加するので、垂直下向きの単位ベクトルは (0, 1)
vertical = np.array([0, 1])
vec_abd = l_elb - l_shoul  # 肩から肘へのベクトル
left_abd_ang_all = 180-np.array([ calangle(vec_abd[i], vertical) for i in range(n_frames) ])
left_max_abd = np.max(left_abd_ang_all)
#最大外転のタイムフレーム
left_max_tmg = np.argmax(left_abd_ang_all)
# 左肩挙上角：右肩と左肩のベクトルと、水平右向きベクトルとの角度
# ※水平右向きの単位ベクトルは (1, 0)
horizontal = np.array([1, 0])
vec_elev = r_shoul - l_shoul
# 角度計算
left_elev_ang_all = 180-np.array([ calangle(vec_elev[i], horizontal) for i in range(n_frames) ])
left_max_elev = np.max(left_elev_ang_all)

# ------------------------------
# 補正：参照フレームの mid_head を原点にする
# ------------------------------
ref_frame = 0  # 補正に用いるフレーム（必要に応じて変更）
ref_mid_head = mid_head[ref_frame]

# 補正後の各部位の座標（ref_frame で描画）
head_corr    = mid_head[ref_frame] - ref_mid_head  # (0,0)
l_shoul_corr = l_shoul[ref_frame] - ref_mid_head
l_elb_corr   = l_elb[ref_frame]   - ref_mid_head
l_wri_corr   = l_wri[ref_frame]   - ref_mid_head
r_shoul_corr = r_shoul[ref_frame] - ref_mid_head
# ------------------------------
# スティックピクチャ描画（左上肢のみ）
# ------------------------------
fig, ax = plt.subplots(figsize=(6,6))
ax.set_xlim(-300, 300)
ax.set_ylim(-300, 300)
ax.set_xlabel("X (px)")
ax.set_ylabel("Y (px)")
ax.set_title("左上肢スティックピクチャ")

# 各部位をプロット（補正後の座標）
ax.scatter(head_corr[0], head_corr[1], color='magenta', s=300, label='Head center',alpha = 0.2)
ax.scatter(r_shoul_corr[0], r_shoul_corr[1], color='gray', s=100, label='Left Shoulder',alpha = 0.2)
ax.scatter(l_shoul_corr[0], l_shoul_corr[1], color='gray', s=100, label='Left Shoulder',alpha = 0.2)
ax.scatter(l_elb_corr[0], l_elb_corr[1], color='gray', s=100, label='Left Elbow',alpha = 0.2)
ax.scatter(l_wri_corr[0], l_wri_corr[1], color='crimson', s=100, label='Left Wrist',alpha = 0.2)
# 部位間を線で接続
ax.plot([l_shoul_corr[0], r_shoul_corr[0]], [l_shoul_corr[1], r_shoul_corr[1]], color='gray', linewidth=2,alpha = 0.2)
ax.plot([l_shoul_corr[0], l_elb_corr[0]], [l_shoul_corr[1], l_elb_corr[1]], color='gray', linewidth=2,alpha = 0.2)
ax.plot([l_elb_corr[0], l_wri_corr[0]], [l_elb_corr[1], l_wri_corr[1]], color='gray', linewidth=2,alpha = 0.2)

#最大外転時の座標系
head_corr2    = mid_head[left_max_tmg] - ref_mid_head  # (0,0)
l_shoul_corr2 = l_shoul[left_max_tmg] - ref_mid_head
l_elb_corr2   = l_elb[left_max_tmg]   - ref_mid_head
l_wri_corr2   = l_wri[left_max_tmg]   - ref_mid_head
r_shoul_corr2 = r_shoul[left_max_tmg] - ref_mid_head


# 各部位をプロット（最大外転時の座標）
ax.scatter(head_corr2[0], head_corr2[1], color='magenta', s=300, label='Head center',alpha = 0.8)
ax.scatter(r_shoul_corr2[0], r_shoul_corr2[1], color='gray', s=100, label='Left Shoulder',alpha = 0.8)
ax.scatter(l_shoul_corr2[0], l_shoul_corr2[1], color='gray', s=100, label='Left Shoulder',alpha = 0.8)
ax.scatter(l_elb_corr2[0], l_elb_corr2[1], color='gray', s=100, label='Left Elbow',alpha = 0.8)
ax.scatter(l_wri_corr2[0], l_wri_corr2[1], color='crimson', s=100, label='Left Wrist',alpha = 0.8)
# 部位間を線で接続
ax.plot([l_shoul_corr2[0], r_shoul_corr2[0]], [l_shoul_corr2[1], r_shoul_corr2[1]], color='gray', linewidth=2,alpha = 0.8)
ax.plot([l_shoul_corr2[0], l_elb_corr2[0]], [l_shoul_corr2[1], l_elb_corr2[1]], color='gray', linewidth=2,alpha = 0.8)
ax.plot([l_elb_corr2[0], l_wri_corr2[0]], [l_elb_corr2[1], l_wri_corr2[1]], color='gray', linewidth=2,alpha = 0.8)

# ------------------------------
# 最大肩外転、最大肩挙上のテキストを描画
# ------------------------------
# ※テキストは全フレームで算出した値を使用（単位は度）
ax.text(-280, 230, f"最大肩外転 = {left_max_abd:.1f}°", fontsize=14, color='black')
ax.text(-280, 180, f"最大肩挙上 = {left_max_elev:.1f}°", fontsize=14, color='black')

ax.grid(alpha =0.2)

#####ここから右上肢の解析#####


r_vec_abd = r_elb - r_shoul  # 肩から肘へのベクトル
right_abd_ang_all = 180-np.array([ calangle(r_vec_abd[i], vertical) for i in range(n_frames) ])
right_max_abd = np.max(right_abd_ang_all)
#最大外転のタイムフレーム
right_max_tmg = np.argmax(right_abd_ang_all)
# 右肩挙上角：右肩と左肩のベクトルと、水平右向きベクトルとの角度
# ※水平右向きの単位ベクトルは (1, 0)
horizontal = np.array([1, 0])
r_vec_elev = l_shoul - r_shoul
# 角度計算
right_elev_ang_all = np.array([ calangle(r_vec_elev[i], horizontal) for i in range(n_frames) ])
right_max_elev = np.max(right_elev_ang_all)

# ------------------------------
# 補正：参照フレームの mid_head を原点にする
# ------------------------------
ref_frame = 0  # 補正に用いるフレーム（必要に応じて変更）
ref_mid_head = mid_head[ref_frame]

# 補正後の各部位の座標（ref_frame で描画）
head_corr    = mid_head[ref_frame] - ref_mid_head 
l_shoul_corr = l_shoul[ref_frame] - ref_mid_head
r_elb_corr   = r_elb[ref_frame]   - ref_mid_head
r_wri_corr   = r_wri[ref_frame]   - ref_mid_head
r_shoul_corr = r_shoul[ref_frame] - ref_mid_head
# ------------------------------
# スティックピクチャ描画（右上肢のみ）
# ------------------------------
fig, ax = plt.subplots(figsize=(6,6))
ax.set_xlim(-300, 300)
ax.set_ylim(-300, 300)
ax.set_xlabel("X (px)")
ax.set_ylabel("Y (px)")
ax.set_title("右上肢スティックピクチャ")

# 各部位をプロット
ax.scatter(head_corr[0], head_corr[1], color='magenta', s=300, label='Head center',alpha = 0.2)
ax.scatter(r_shoul_corr[0], r_shoul_corr[1], color='gray', s=100, label='Left Shoulder',alpha = 0.2)
ax.scatter(l_shoul_corr[0], l_shoul_corr[1], color='gray', s=100, label='Left Shoulder',alpha = 0.2)
ax.scatter(r_elb_corr[0], r_elb_corr[1], color='gray', s=100, label='Left Elbow',alpha = 0.2)
ax.scatter(r_wri_corr[0], r_wri_corr[1], color='crimson', s=100, label='Left Wrist',alpha = 0.2)
# 部位間を線で接続
ax.plot([l_shoul_corr[0], r_shoul_corr[0]], [l_shoul_corr[1], r_shoul_corr[1]], color='gray', linewidth=2,alpha = 0.2)
ax.plot([r_shoul_corr[0], r_elb_corr[0]], [r_shoul_corr[1], r_elb_corr[1]], color='gray', linewidth=2,alpha = 0.2)
ax.plot([r_elb_corr[0], r_wri_corr[0]], [r_elb_corr[1], r_wri_corr[1]], color='gray', linewidth=2,alpha = 0.2)

#最大外転時の座標系
head_corr2    = mid_head[left_max_tmg] - ref_mid_head 
l_shoul_corr2 = l_shoul[left_max_tmg] - ref_mid_head
r_elb_corr2   = r_elb[left_max_tmg]   - ref_mid_head
r_wri_corr2   = r_wri[left_max_tmg]   - ref_mid_head
r_shoul_corr2 = r_shoul[left_max_tmg] - ref_mid_head


# 各部位をプロット（最大外転時の座標）
ax.scatter(head_corr2[0], head_corr2[1], color='magenta', s=300, label='Head center',alpha = 0.8)
ax.scatter(r_shoul_corr2[0], r_shoul_corr2[1], color='gray', s=100, label='Left Shoulder',alpha = 0.8)
ax.scatter(l_shoul_corr2[0], l_shoul_corr2[1], color='gray', s=100, label='Left Shoulder',alpha = 0.8)
ax.scatter(r_elb_corr2[0], r_elb_corr2[1], color='gray', s=100, label='Left Elbow',alpha = 0.8)
ax.scatter(r_wri_corr2[0], r_wri_corr2[1], color='crimson', s=100, label='Left Wrist',alpha = 0.8)
# 部位間を線で接続
ax.plot([l_shoul_corr2[0], r_shoul_corr2[0]], [l_shoul_corr2[1], r_shoul_corr2[1]], color='gray', linewidth=2,alpha = 0.8)
ax.plot([r_shoul_corr2[0], r_elb_corr2[0]], [r_shoul_corr2[1], r_elb_corr2[1]], color='gray', linewidth=2,alpha = 0.8)
ax.plot([r_elb_corr2[0], r_wri_corr2[0]], [r_elb_corr2[1], r_wri_corr2[1]], color='gray', linewidth=2,alpha = 0.8)

# ------------------------------
# 最大肩外転、最大肩挙上のテキストを描画
# ------------------------------
# ※テキストは全フレームで算出した値を使用（単位は度）
ax.text(-280, 230, f"最大肩外転 = {right_max_abd:.1f}°", fontsize=14, color='black')
ax.text(-280, 180, f"最大肩挙上 = {right_max_elev:.1f}°", fontsize=14, color='black')

ax.grid(alpha =0.2)
plt.show()

このあたりの細かい描画の説明については、また別の記事で細かく紹介していこうと思っています。

✅ 結果：スティックピクチャでの比較

以下の図のように：

手前：最大外転時の骨格ライン
色の濃さで動きの変化を視覚化
上部に最大外転角・挙上角を数値表示

が行われます。これは前回記事のサンプル動画の肩関節外転動作の数値化です。薄いのが動作開始前、濃い色のほうが最大外転時の動作の瞬間です。

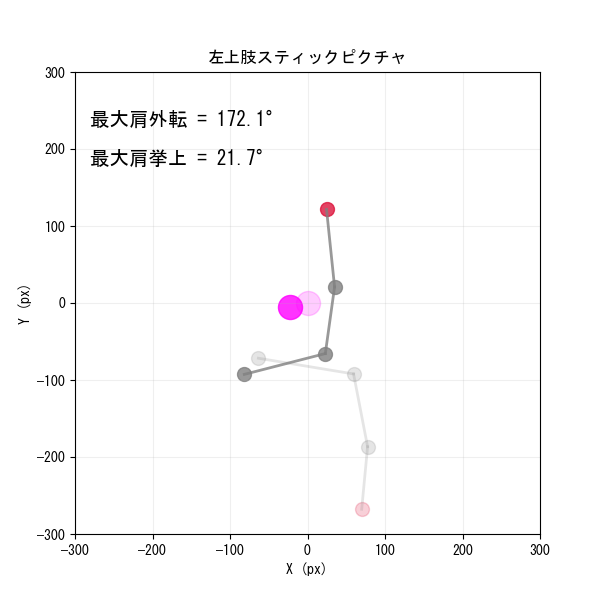
左右それぞれの図が別ウィンドウで出力されます。そのため、右上肢で肩関節外転をした場合でも、左上肢で肩関節外転をした場合でも大丈夫です。

✅ まとめ

今回は以下の処理を行うコードを書きました。肩関節外転は、Manual Function Testにも含まれている動作項目であるため、比較的評価としても使いやすいのではないかと考えています。

またカメラ平面上での動作であれば外転動作に限らず肩関節屈曲動作なども同じように定量化できます（具体例としては、横から対象者を撮影する）

外転と肩峰挙上に限局していますが、頭部や体幹の側屈などまだまだ加えられる要素はあると思っています。関節角度の数字そのものに加えて、代償動作を合わせてみることが重要だと最近実感しております💦。

※あくまでも動画からの推定になります。精度は撮影環境や服装（背景と服装の色のコントラストはあたほうが良い印象）などにも依存します。

ポイント	内容
✅ MediaPipeの出力CSVから可動域を算出	csvデータの読み込み+関節座標の定義
✅ 垂直・水平ベクトルとのなす角で定量化	ベクトルを用いた角度計算
✅ スティックピクチャで動作の差を直感的に可視化	matplotlib（グラフ描画パッケージ）を用いたグラフィックス